研究の依頼をされる際には、 製品の効果を検出することを主な目的としていることが多いと思います。ここでは、「科学的に効果がある」ということを説明させて頂きたいと思います。臨床試験を実施する際の統計手法について、ご参考になれば幸いです。
統計の基本的な考え方
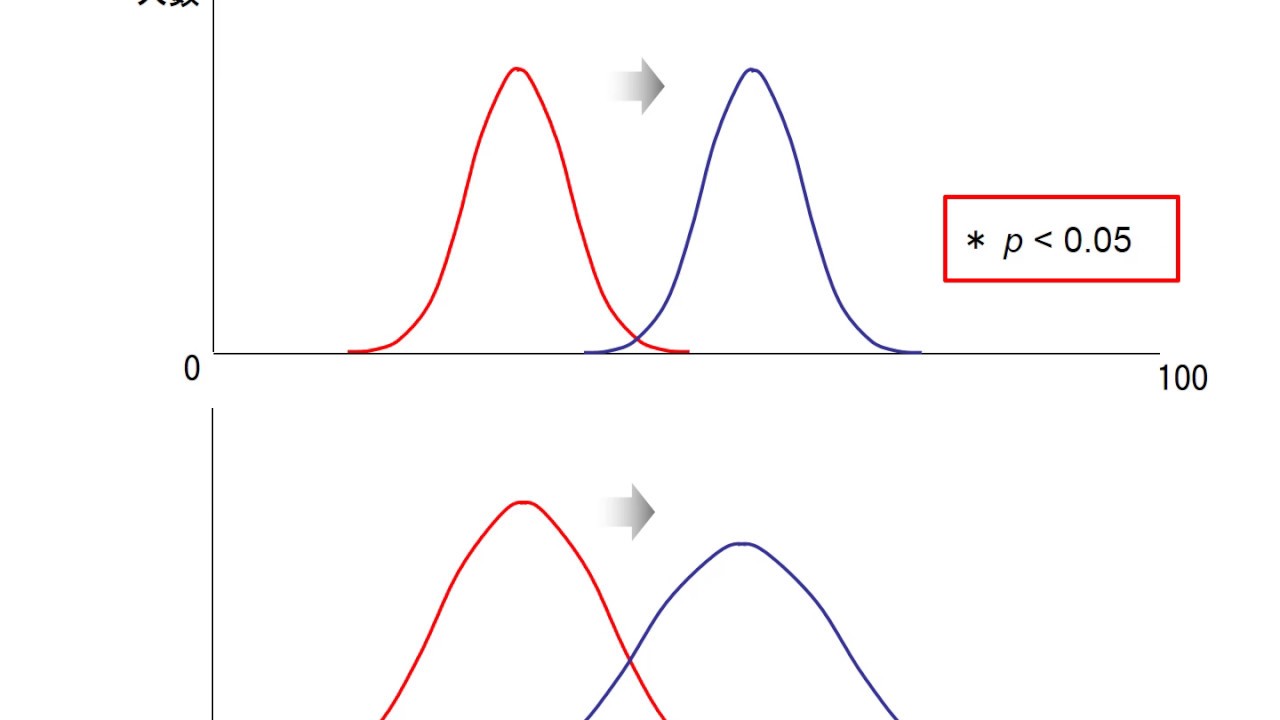
効果の検出は確率統計の考え方が基本にあり、統計解析によって判断がなされます。その基本的な考え方を動画にしてみました(機械音声によるパワーポイントファイルの説明になります)。
「科学的に効果がある」というのは、確率論であり、曖昧であり、 慣習によって決まっていることが分かるかと思います。突き詰めても「100%効果がある」ということは難しいです。
統計解析の手法
私が学生の頃は、Excelで実施可能な統計解析で許されていましたが、現在は、特別なソフトウェアを必要とする場合が多いです。
統計解析の動画解説
どのような場合に、どのような統計解析をすれば良いか、これも動画にしみました。
検討したいことが多くあっても、効果を検出しやすいパターンに当てはめることが、良い結果を導くコツの1つです。 難しく考えない、ブラックボックスを追求しないことが、理解のコツだと考えています。
2つの平均値を比較するt検定
2つの平均値を比較するのはExcelでも可能で(TTEST関数)、t検定と呼ばれる解析を利用します。最も効果を検出しやすい解析方法であり、なるべくt検定を使える研究計画にすることをお勧めしています。
一般的な健康食品や化粧品などの効果検証では、製品とプラセボの2つを比較しますが、使用前と使用後も含めると、2×2=4つの平均値があります。この場合、使い勝手の良いt検定の適用はルール違反となり、分散分析が必要になります。
分散分析のルール
3つ以上の平均値を比較する際、まずは分散分析を利用することが求められています。AとB、BとC、CとAといった具合に、2つの数値を比較するよりも3倍効果が出やすくなります。それはズルいのでルール違反!といったイメージです。
私共が報告する際には、まずはt検定の数値を提示して、有効性の見込みをお伝えすることが多いです。論文化や機能性表示をする際には、分散分析での有意差が必要となります(実際は、分散分析で差があればt検定を実施する進め方がサイエンスのルールです)。より高度な統計解析もありますが、まずは「t検定」と「分散分析」を知っておくと、基本的な解釈も分かりやすくなるかと思います。
計画時点から統計解析を意識する重要性
このように説明すると、絶対的な真理がないように混乱される場合があります。 実際は、製品を使用される各個人に効果があることが真実であり、 サイエンスはそれを上手く数値化することが使命であると考えています。
3群の比較(プラセボと製品2用量)は効果を検出することが難しくその説明に苦慮することもしばしばありました。このページや動画の説明で、2用量にすべきである(加えて、中間測定を複数設けず前後のみにすべきである)ことがご理解頂けるかと思います。検討したいことが複雑な場合も、それらを上手くシンプルに分解して、 効果を最大限に出やすくすることをお勧めしています。