測定誤差と信頼区間
では、測定値から誤差を示す方法はあるのでしょうか。

データのばらつきなどを求める際によく利用されるのが、この統計学カテゴリー度々ご紹介している標準偏差や標準誤差です。あらためてこれらをデータにおけるどの役割を持っているのか確認していきましょう。
標準偏差・標準誤差・信頼区間
まずは標準偏差についてです。
標準偏差とはエクセルの関数STDEVなどによって求めることが出来るのですが、この値はそのデータの標準偏差、つまり標準的な平均との差を表しています。
次に信頼区間とはある測定から推定される繰り返し測定の測定値出現の範囲を示しており、通常、95%信頼限界とされています。この意味するものは、母集団から標本(データ)を取りだし、その平均から95%信頼区間を求める、という作業を100回やったときに、95回はその区間の中に母平均が含まれますよ、といった頻度もしくは割合を指しているのです。
最後に標準誤差とは測定値から推定される平均値の標準偏差のことを指し間接的な値となります。

信頼区間の計算方法
数が少ない測定値からその測定全体の信頼度(信頼区間)、いわゆる測定誤差範囲を示す方法をご紹介いたします。

まず測定回数(n)が十分に多く、その測定値のばらつきが95%の信頼限界で正規分布しているとき、
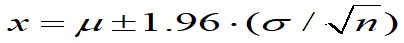
の式で求めることが出来、この値は測定値ではなく、平均値がどのくらいばらつくか(標準誤差)を示す為、標準偏差を√n(測定回数の平方根)で割っているのです。
次に、測定回数(n)が少なく、正規分布を予測しなければならないとき、
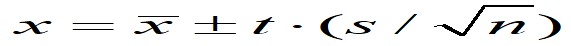
の式で求めることが出来ます。この式は(n)を(n-1)にて使用されており、nの値が大きくなるにつれほぼ等しい値を示すようになります。
これらの式から求められる値はエクセルの中で関数TINVで求めることが出来ます。もしくは以下のような表を活用してその数値を参照します。
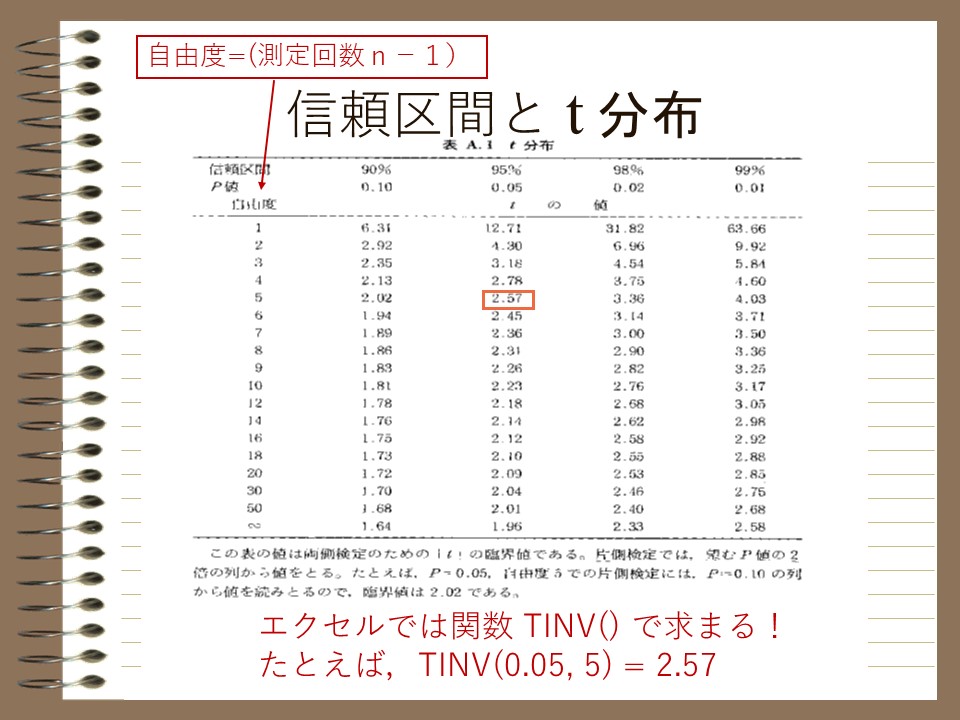
95%信頼区間(x)は、例数(n)が十分大きい数になると、概ね平均値±2SD(標準誤差)の範囲になることが分かるかと思います。
上記の表より、例数が十分に大きくなくても信頼区間に大きな差がないことが分かります。自由度が18(=例数が19)の際に平均値±2.1SD、自由度が11(=例数が12)の際に平均値±2.2SD程度といった具合で、例数が2桁あれば例数無限大と大きく変わらない信頼区間の設定が可能であることが分かります。
正規分布に表すと、以下のような関係になります。
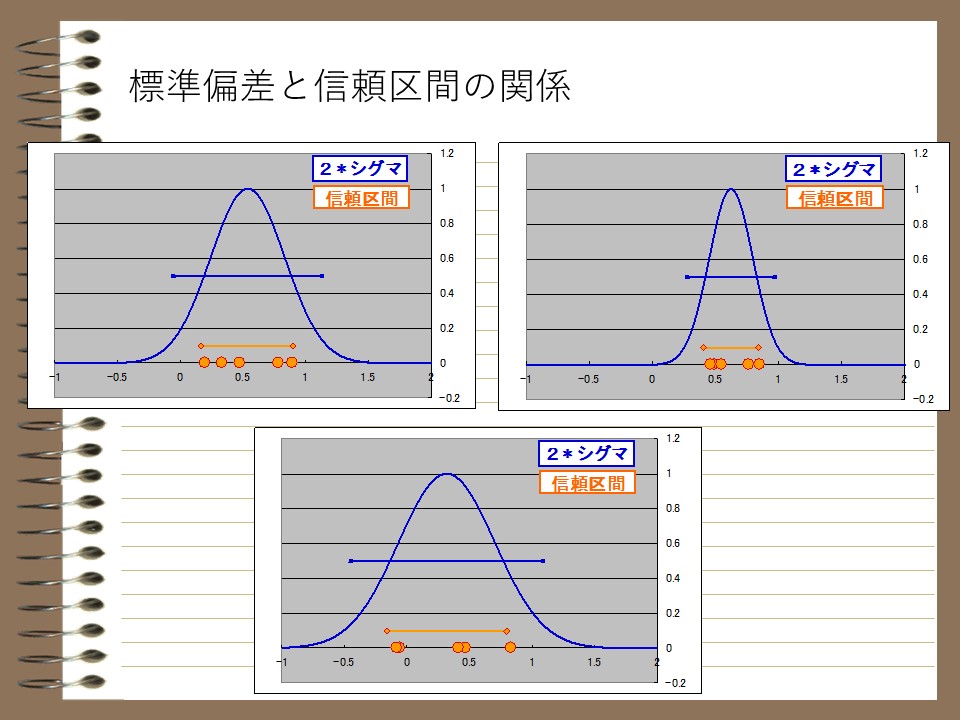
異常値と棄却判定
最後に異常値と棄却判定についてご紹介いたします。
母集団の数値が正規分布すると仮定できると,Q=|疑わしい値-最近接値|/|最大値-最小値|といったディクソンのQとして,測定値を評価し,棄却判定に利用することができます。この値Qが以下の表にある臨界値を超えた際には、その値が異常値として棄却判定できます。

練習問題
以下、信頼区間や棄却判定に関する演習問題になります。ダウンロードしてチャレンジしてみてください。




